Maquinas de soporte vectorial, (Support vector machine SVM)
Contents
Maquinas de soporte vectorial, (Support vector machine SVM)¶
Las maquinas de soporte vectorial se pueden definir como:
Clasfiicar lineal de orden maximo
Clasificador lineal en un espacio N-dimensional
Entendamos la intuición detras de estos dos conceptos.
Nuestra funcion de coste esta definda como sigue:
Si suponemos que $y=1$ y $y=0$ tenemos para estos dos casos que:
#Cost function
h = lambda z: 1/(1+np.exp(-z))
J1 = lambda z,y: -y*np.log(h(z))
J2 = lambda z,y: -(1-y)*np.log(1-h(z))
# Ref metricas
m1 = lambda z: z-1
#===================
z1 = np.linspace(-2, 10)
z2 = np.linspace(-10, 2)
plt.plot(z1,J1(z1,1), label="y=1")
plt.plot(z2,J2(z2,0), label="y=0")
plt.legend()
plt.xlabel("Z")
plt.ylabel("Cost function")
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Input In [1], in <cell line: 12>()
7 m1 = lambda z: z-1
11 #===================
---> 12 z1 = np.linspace(-2, 10)
13 z2 = np.linspace(-10, 2)
14 plt.plot(z1,J1(z1,1), label="y=1")
NameError: name 'np' is not defined
Para $y = 1$ se cumple que para $Z=\theta^T X\geq 0$ la clasificacion será tipo 1
Para $y = 0$ se cumple que para $Z=\theta^T X < 0 $ la clasificación será tipo 0
Las métricas anteriores pueden ser definidas en términos de métricas que permitan clasificar en los siguiente intervalos, segun la curva roja y negra definida en la gráfica:
Para $y = 1$ se cumple que para $Z=\theta^T X\geq 1$ la clasificacion será tipo 1
Para $y = 0$ se cumple que para $Z=\theta^T X < 1 $ la clasificación será tipo 0
Si interpretamos la funcion $J(\theta)$ como:
$J(\theta)=A+\lambda B$, podemos rescribir la anterior expresión como:
$J(\theta)=C A’+B’$
Siendo $C=\frac{1}{\lambda}$, el inverso del parametros de regularación descrito en las sesiones anteriores.
Nuestro objetivo sera mínimizar la función $\min [J(\theta))] =\min[ C A’+B’]$,
El termino B’ de la anterior expresión puede ser expresado como sigue:
$B’ = \frac{1}{2}\sum_{j=1}^{n}\theta_j^2=\frac{1}{2} (\theta_1^2 + \theta_2^2+…+\theta_n^2)=\frac{1}{2}||\theta||^2$
Interpretacion geométrica¶
Supongamos que tenemos dos caracteristicas, en nuestro sistema, de esta manera tenemos que:
$\theta^T X= [\theta_1, \theta_2] [x1,x2]$
Continuar con los aspectos teóricos…
References [1] https://www.cienciadedatos.net/documentos/34_maquinas_de_vector_soporte_support_vector_machines
import numpy as np
import matplotlib.pylab as plt
from sklearn.datasets import make_moons
from sklearn.datasets import make_circles
from sklearn.datasets import make_blobs
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
# Libraries for draw contours
def make_meshgrid(x, y, h=0.02):
"""Create a mesh of points to plot in
Parameters
----------
x: data to base x-axis meshgrid on
y: data to base y-axis meshgrid on
h: stepsize for meshgrid, optional
Returns
-------
xx, yy : ndarray
"""
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Parameters
----------
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
def plot_contoursExact(ax, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Parameters
----------
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
# Dataset Toys References
# https://scikit-learn.org/stable/datasets/toy_dataset.html
# https://matplotlib.org/stable/gallery/subplots_axes_and_figures/subplots_demo.html
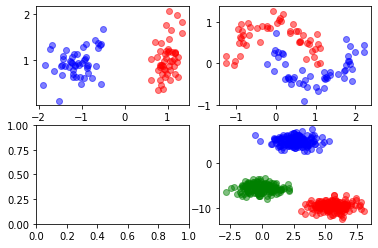
# Dataset sinteticos
X0, y0 = make_classification(
n_features=2, n_redundant=0, n_informative=2, random_state=1,
n_clusters_per_class=1
)
X1, y1 = make_moons(n_samples=100, noise=0.15, shuffle=True, random_state=1)
X2, y2 = make_circles(n_samples=100, noise=0.05, shuffle=True, random_state=1)
X3, y3 = make_blobs(n_samples=500, centers=3, n_features=2,shuffle=True,
random_state=10)
fig, axs = plt.subplots(2,2)
axs[0, 0].plot(X0[:,0][y0==0],X0[:,1][y0==0],"ro", alpha=0.5)
axs[0, 0].plot(X0[:,0][y0==1],X0[:,1][y0==1],"bo", alpha=0.5)
# Dataset a moons
axs[0, 1].plot(X1[:,0][y1==0],X1[:,1][y1==0],"ro", alpha=0.5)
axs[0, 1].plot(X1[:,0][y1==1],X1[:,1][y1==1],"bo", alpha=0.5)
# Dataset circles
axs[1, 0].plot(X2[:,0][y2==0],X2[:,1][y2==0],"ro", alpha=0.5)
axs[1, 0].plot(X2[:,0][y2==1],X2[:,1][y2==1],"bo", alpha=0.5)
# Dataset circles
axs[1, 1].plot(X3[:,0][y3==0],X3[:,1][y3==0],"ro", alpha=0.5)
axs[1, 1].plot(X3[:,0][y3==1],X3[:,1][y3==1],"bo", alpha=0.5)
axs[1, 1].plot(X3[:,0][y3==2],X3[:,1][y3==2],"go", alpha=0.5)
[<matplotlib.lines.Line2D at 0x7f8a33581950>]
# Based on :
# https://rramosp.github.io/ai4eng.v1.20211.udea/content/NOTES%2003.03%20-%20SVM%20AND%20FEATURE%20TRANSFORMATION.html
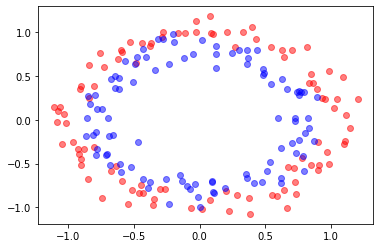
X, y = make_circles(n_samples=200, noise=0.1, shuffle=True, random_state=1)
plt.plot(X[:,0][y==0],X[:,1][y==0],"ro", alpha=0.5)
plt.plot(X[:,0][y==1],X[:,1][y==1],"bo", alpha=0.5)
[<matplotlib.lines.Line2D at 0x7f8a34d03310>]
clf = SVC(gamma = 0.10) #Complexity of algorithm
clf.fit(X, y)
#Countour plot
fig, ax = plt.subplots()
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
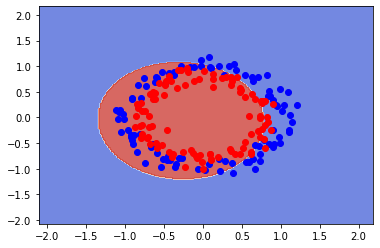
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
plt.plot(X[y==0][:,0],X[y==0][:,1],"bo", alpha=1)
plt.plot(X[y==1][:,0],X[y==1][:,1],"ro", alpha=1)
print(f"Training error:{clf.score(X, y):.3f}")
Training error:0.635
Grid Search of parameter in SVM¶
Grid-search is used to find the optimal hyperparameters of a model which results in the most ‘accurate’ predictions. https://towardsdatascience.com/grid-search-for-model-tuning-3319b259367e
#https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html
from sklearn.model_selection import GridSearchCV
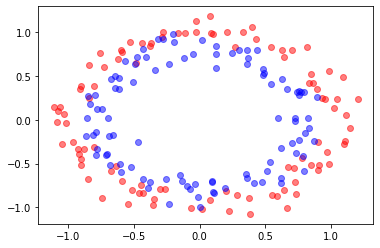
X, y = make_circles(n_samples=200, noise=0.1, shuffle=True, random_state=1)
plt.plot(X[:,0][y==0],X[:,1][y==0],"ro", alpha=0.5)
plt.plot(X[:,0][y==1],X[:,1][y==1],"bo", alpha=0.5)
[<matplotlib.lines.Line2D at 0x7f8a349f4250>]
parameters = {'kernel':('linear', 'rbf'), 'C':[1, 10]}
parameters = {'C': [0.1,1, 10, 100], 'gamma': [1,0.1,0.01,0.001],'kernel': ['rbf', 'poly', 'sigmoid']}
clf = GridSearchCV(estimator=SVC(),
param_grid = parameters)
clf.fit(X, y)
sorted(clf.cv_results_.keys())
['mean_fit_time',
'mean_score_time',
'mean_test_score',
'param_C',
'param_gamma',
'param_kernel',
'params',
'rank_test_score',
'split0_test_score',
'split1_test_score',
'split2_test_score',
'split3_test_score',
'split4_test_score',
'std_fit_time',
'std_score_time',
'std_test_score']
clf.cv_results_
{'mean_fit_time': array([0.00206857, 0.00133414, 0.002145 , 0.00184765, 0.00131226,
0.00177274, 0.00177774, 0.00132613, 0.00178552, 0.00216789,
0.0015471 , 0.00219789, 0.00242796, 0.00140429, 0.00226235,
0.00185962, 0.00131516, 0.0017982 , 0.00191288, 0.00132165,
0.0017786 , 0.00210128, 0.00132256, 0.00177875, 0.00141177,
0.00170116, 0.00228949, 0.00174408, 0.00135508, 0.00191026,
0.00188537, 0.00132656, 0.00182943, 0.00191078, 0.00135727,
0.00183592, 0.00172868, 0.00411572, 0.00180178, 0.00154214,
0.00128736, 0.00196505, 0.00184169, 0.00172501, 0.00232635,
0.00182514, 0.00139742, 0.00196843]),
'mean_score_time': array([0.00094509, 0.00056295, 0.00075049, 0.00090499, 0.00057168,
0.00067277, 0.00086918, 0.00056782, 0.00071511, 0.00105624,
0.00064454, 0.00091519, 0.00112543, 0.00056086, 0.00075355,
0.00091472, 0.00056481, 0.00069489, 0.00093093, 0.0005722 ,
0.0006752 , 0.00095043, 0.00056782, 0.00070267, 0.000664 ,
0.00056734, 0.00107045, 0.0008214 , 0.00061026, 0.00069866,
0.00095572, 0.00059428, 0.00069923, 0.00090742, 0.00056558,
0.00067677, 0.00058112, 0.00057974, 0.00058169, 0.00066299,
0.0005559 , 0.00066509, 0.0008719 , 0.00080714, 0.00087495,
0.00087662, 0.00057192, 0.00074143]),
'mean_test_score': array([0.535, 0.545, 0.375, 0.45 , 0.555, 0.37 , 0.41 , 0.555, 0.37 ,
0.37 , 0.555, 0.37 , 0.84 , 0.495, 0.485, 0.455, 0.555, 0.37 ,
0.41 , 0.555, 0.37 , 0.37 , 0.555, 0.37 , 0.865, 0.485, 0.52 ,
0.835, 0.555, 0.385, 0.42 , 0.555, 0.37 , 0.37 , 0.555, 0.37 ,
0.845, 0.48 , 0.5 , 0.865, 0.545, 0.39 , 0.445, 0.555, 0.385,
0.38 , 0.555, 0.37 ]),
'param_C': masked_array(data=[0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1,
0.1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 10, 10, 10,
10, 10, 10, 10, 10, 10, 10, 10, 10, 100, 100, 100, 100,
100, 100, 100, 100, 100, 100, 100, 100],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False],
fill_value='?',
dtype=object),
'param_gamma': masked_array(data=[1, 1, 1, 0.1, 0.1, 0.1, 0.01, 0.01, 0.01, 0.001, 0.001,
0.001, 1, 1, 1, 0.1, 0.1, 0.1, 0.01, 0.01, 0.01, 0.001,
0.001, 0.001, 1, 1, 1, 0.1, 0.1, 0.1, 0.01, 0.01, 0.01,
0.001, 0.001, 0.001, 1, 1, 1, 0.1, 0.1, 0.1, 0.01,
0.01, 0.01, 0.001, 0.001, 0.001],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False],
fill_value='?',
dtype=object),
'param_kernel': masked_array(data=['rbf', 'poly', 'sigmoid', 'rbf', 'poly', 'sigmoid',
'rbf', 'poly', 'sigmoid', 'rbf', 'poly', 'sigmoid',
'rbf', 'poly', 'sigmoid', 'rbf', 'poly', 'sigmoid',
'rbf', 'poly', 'sigmoid', 'rbf', 'poly', 'sigmoid',
'rbf', 'poly', 'sigmoid', 'rbf', 'poly', 'sigmoid',
'rbf', 'poly', 'sigmoid', 'rbf', 'poly', 'sigmoid',
'rbf', 'poly', 'sigmoid', 'rbf', 'poly', 'sigmoid',
'rbf', 'poly', 'sigmoid', 'rbf', 'poly', 'sigmoid'],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False],
fill_value='?',
dtype=object),
'params': [{'C': 0.1, 'gamma': 1, 'kernel': 'rbf'},
{'C': 0.1, 'gamma': 1, 'kernel': 'poly'},
{'C': 0.1, 'gamma': 1, 'kernel': 'sigmoid'},
{'C': 0.1, 'gamma': 0.1, 'kernel': 'rbf'},
{'C': 0.1, 'gamma': 0.1, 'kernel': 'poly'},
{'C': 0.1, 'gamma': 0.1, 'kernel': 'sigmoid'},
{'C': 0.1, 'gamma': 0.01, 'kernel': 'rbf'},
{'C': 0.1, 'gamma': 0.01, 'kernel': 'poly'},
{'C': 0.1, 'gamma': 0.01, 'kernel': 'sigmoid'},
{'C': 0.1, 'gamma': 0.001, 'kernel': 'rbf'},
{'C': 0.1, 'gamma': 0.001, 'kernel': 'poly'},
{'C': 0.1, 'gamma': 0.001, 'kernel': 'sigmoid'},
{'C': 1, 'gamma': 1, 'kernel': 'rbf'},
{'C': 1, 'gamma': 1, 'kernel': 'poly'},
{'C': 1, 'gamma': 1, 'kernel': 'sigmoid'},
{'C': 1, 'gamma': 0.1, 'kernel': 'rbf'},
{'C': 1, 'gamma': 0.1, 'kernel': 'poly'},
{'C': 1, 'gamma': 0.1, 'kernel': 'sigmoid'},
{'C': 1, 'gamma': 0.01, 'kernel': 'rbf'},
{'C': 1, 'gamma': 0.01, 'kernel': 'poly'},
{'C': 1, 'gamma': 0.01, 'kernel': 'sigmoid'},
{'C': 1, 'gamma': 0.001, 'kernel': 'rbf'},
{'C': 1, 'gamma': 0.001, 'kernel': 'poly'},
{'C': 1, 'gamma': 0.001, 'kernel': 'sigmoid'},
{'C': 10, 'gamma': 1, 'kernel': 'rbf'},
{'C': 10, 'gamma': 1, 'kernel': 'poly'},
{'C': 10, 'gamma': 1, 'kernel': 'sigmoid'},
{'C': 10, 'gamma': 0.1, 'kernel': 'rbf'},
{'C': 10, 'gamma': 0.1, 'kernel': 'poly'},
{'C': 10, 'gamma': 0.1, 'kernel': 'sigmoid'},
{'C': 10, 'gamma': 0.01, 'kernel': 'rbf'},
{'C': 10, 'gamma': 0.01, 'kernel': 'poly'},
{'C': 10, 'gamma': 0.01, 'kernel': 'sigmoid'},
{'C': 10, 'gamma': 0.001, 'kernel': 'rbf'},
{'C': 10, 'gamma': 0.001, 'kernel': 'poly'},
{'C': 10, 'gamma': 0.001, 'kernel': 'sigmoid'},
{'C': 100, 'gamma': 1, 'kernel': 'rbf'},
{'C': 100, 'gamma': 1, 'kernel': 'poly'},
{'C': 100, 'gamma': 1, 'kernel': 'sigmoid'},
{'C': 100, 'gamma': 0.1, 'kernel': 'rbf'},
{'C': 100, 'gamma': 0.1, 'kernel': 'poly'},
{'C': 100, 'gamma': 0.1, 'kernel': 'sigmoid'},
{'C': 100, 'gamma': 0.01, 'kernel': 'rbf'},
{'C': 100, 'gamma': 0.01, 'kernel': 'poly'},
{'C': 100, 'gamma': 0.01, 'kernel': 'sigmoid'},
{'C': 100, 'gamma': 0.001, 'kernel': 'rbf'},
{'C': 100, 'gamma': 0.001, 'kernel': 'poly'},
{'C': 100, 'gamma': 0.001, 'kernel': 'sigmoid'}],
'rank_test_score': array([19, 17, 36, 27, 6, 37, 30, 6, 37, 37, 6, 37, 4, 22, 23, 26, 6,
37, 30, 6, 37, 37, 6, 37, 1, 23, 20, 5, 6, 33, 29, 6, 37, 37,
6, 37, 3, 25, 21, 1, 17, 32, 28, 6, 33, 35, 6, 37],
dtype=int32),
'split0_test_score': array([0.275, 0.525, 0.25 , 0.3 , 0.575, 0.25 , 0.25 , 0.575, 0.25 ,
0.25 , 0.575, 0.25 , 0.9 , 0.45 , 0.425, 0.275, 0.575, 0.25 ,
0.25 , 0.575, 0.25 , 0.25 , 0.575, 0.25 , 0.9 , 0.325, 0.525,
0.775, 0.575, 0.275, 0.275, 0.575, 0.25 , 0.25 , 0.575, 0.25 ,
0.9 , 0.325, 0.525, 0.925, 0.525, 0.275, 0.3 , 0.575, 0.275,
0.275, 0.575, 0.25 ]),
'split1_test_score': array([0.55 , 0.5 , 0.4 , 0.375, 0.5 , 0.375, 0.375, 0.5 , 0.375,
0.375, 0.5 , 0.375, 0.875, 0.45 , 0.525, 0.425, 0.5 , 0.375,
0.375, 0.5 , 0.375, 0.375, 0.5 , 0.375, 0.875, 0.45 , 0.5 ,
0.875, 0.5 , 0.4 , 0.375, 0.5 , 0.375, 0.375, 0.5 , 0.375,
0.925, 0.45 , 0.45 , 0.875, 0.5 , 0.425, 0.4 , 0.5 , 0.4 ,
0.375, 0.5 , 0.375]),
'split2_test_score': array([0.475, 0.5 , 0.325, 0.375, 0.5 , 0.325, 0.325, 0.5 , 0.325,
0.325, 0.5 , 0.325, 0.75 , 0.35 , 0.55 , 0.375, 0.5 , 0.325,
0.325, 0.5 , 0.325, 0.325, 0.5 , 0.325, 0.725, 0.45 , 0.425,
0.825, 0.5 , 0.325, 0.325, 0.5 , 0.325, 0.325, 0.5 , 0.325,
0.7 , 0.45 , 0.45 , 0.75 , 0.5 , 0.325, 0.375, 0.5 , 0.325,
0.325, 0.5 , 0.325]),
'split3_test_score': array([0.825, 0.575, 0.5 , 0.775, 0.575, 0.525, 0.725, 0.575, 0.525,
0.525, 0.575, 0.525, 0.825, 0.6 , 0.5 , 0.775, 0.575, 0.525,
0.725, 0.575, 0.525, 0.525, 0.575, 0.525, 0.9 , 0.575, 0.6 ,
0.85 , 0.575, 0.525, 0.725, 0.575, 0.525, 0.525, 0.575, 0.525,
0.875, 0.575, 0.55 , 0.875, 0.575, 0.525, 0.725, 0.575, 0.525,
0.525, 0.575, 0.525]),
'split4_test_score': array([0.55 , 0.625, 0.4 , 0.425, 0.625, 0.375, 0.375, 0.625, 0.375,
0.375, 0.625, 0.375, 0.85 , 0.625, 0.425, 0.425, 0.625, 0.375,
0.375, 0.625, 0.375, 0.375, 0.625, 0.375, 0.925, 0.625, 0.55 ,
0.85 , 0.625, 0.4 , 0.4 , 0.625, 0.375, 0.375, 0.625, 0.375,
0.825, 0.6 , 0.525, 0.9 , 0.625, 0.4 , 0.425, 0.625, 0.4 ,
0.4 , 0.625, 0.375]),
'std_fit_time': array([4.98258060e-04, 1.15697184e-04, 1.47676399e-05, 1.12806470e-04,
8.59894873e-06, 2.72885036e-05, 1.31710675e-05, 2.63568046e-05,
1.13863282e-05, 3.79923829e-04, 1.28727929e-04, 5.16469799e-04,
6.73457168e-04, 5.17707705e-05, 1.01321669e-04, 9.34947932e-05,
1.71776574e-05, 1.83439199e-05, 2.41461900e-04, 3.17648715e-05,
6.29172130e-06, 6.04826060e-04, 1.52411955e-05, 1.07617403e-05,
5.03458753e-05, 1.07042816e-04, 4.28722759e-04, 4.31782300e-05,
4.91000127e-05, 8.35848615e-05, 1.48630792e-04, 2.01651948e-05,
5.04984734e-05, 1.35171400e-04, 6.12603815e-05, 1.14898621e-04,
1.64422455e-04, 1.10184680e-03, 5.68245863e-05, 5.73778769e-05,
1.86360992e-05, 1.79204831e-04, 4.44906189e-05, 4.23235499e-04,
5.90832519e-04, 5.77625583e-05, 1.44899852e-04, 3.64501803e-04]),
'std_score_time': array([7.28726689e-05, 2.07467458e-05, 1.40237152e-05, 4.36011199e-05,
1.42823674e-05, 2.10492147e-05, 3.40338158e-05, 6.76806476e-06,
4.20360015e-05, 2.09807613e-04, 3.96330570e-05, 2.02092150e-04,
2.78411109e-04, 1.56454915e-05, 4.18777602e-05, 2.55290973e-05,
1.34945758e-05, 2.43245847e-05, 1.14556949e-04, 1.96396717e-05,
4.48328372e-06, 7.76288257e-05, 1.28202705e-05, 3.19076396e-05,
3.48636122e-05, 1.71214423e-05, 5.96806583e-04, 2.63503337e-05,
6.66796029e-05, 2.11935745e-05, 1.98559024e-05, 1.22544367e-05,
6.48112743e-06, 4.05171314e-05, 1.60201674e-05, 9.61226127e-06,
2.62072236e-05, 9.94819913e-06, 1.76947067e-05, 1.82270341e-05,
2.07375378e-05, 1.36175209e-05, 3.87853611e-05, 1.93202954e-04,
2.08876633e-04, 3.43803890e-05, 1.42105474e-05, 1.60986919e-04]),
'std_test_score': array([0.17649363, 0.0484768 , 0.083666 , 0.16733201, 0.0484768 ,
0.09 , 0.16401219, 0.0484768 , 0.09 , 0.09 ,
0.0484768 , 0.09 , 0.05147815, 0.1029563 , 0.05147815,
0.16911535, 0.0484768 , 0.09 , 0.16401219, 0.0484768 ,
0.09 , 0.09 , 0.0484768 , 0.09 , 0.0717635 ,
0.10559356, 0.05787918, 0.03391165, 0.0484768 , 0.08455767,
0.1584298 , 0.0484768 , 0.09 , 0.09 , 0.0484768 ,
0.09 , 0.07968689, 0.09924717, 0.041833 , 0.06041523,
0.0484768 , 0.08602325, 0.14611639, 0.0484768 , 0.08455767,
0.0842615 , 0.0484768 , 0.09 ])}
clf.best_estimator_
SVC(C=10, gamma=1)
clf.best_params_
{'C': 10, 'gamma': 1, 'kernel': 'rbf'}
clf.best_score_
0.865
#Countour plot
fig, ax = plt.subplots()
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
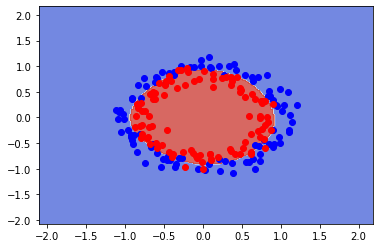
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
plt.plot(X[y==0][:,0],X[y==0][:,1],"bo", alpha=1)
plt.plot(X[y==1][:,0],X[y==1][:,1],"ro", alpha=1)
print(f"Training error:{clf.score(X, y):.3f}")
Training error:0.885
Tarea 11.1
Implementar un SVM para clasificar los siguientes datasets, para ello se deberá crear un grid search.
Con los mejores párametros dibujar las fronteras de clasificación.
X0, y0 = make_classification(
n_features=2, n_redundant=0, n_informative=2, random_state=1,
n_clusters_per_class=1
)
X1, y1 = make_moons(n_samples=100, noise=0.15, shuffle=True, random_state=1)
X3, y3 = make_blobs(n_samples=500, centers=3, n_features=2,shuffle=True, random_state=10)
# Dataset Toys References
# https://scikit-learn.org/stable/datasets/toy_dataset.html
# https://matplotlib.org/stable/gallery/subplots_axes_and_figures/subplots_demo.html
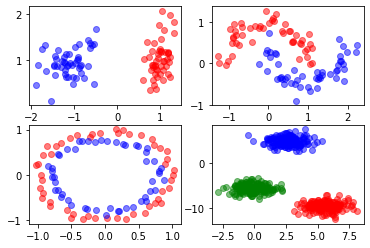
# Dataset sinteticos
X0, y0 = make_classification(
n_features=2, n_redundant=0, n_informative=2, random_state=1,
n_clusters_per_class=1
)
X1, y1 = make_moons(n_samples=100, noise=0.15, shuffle=True, random_state=1)
X2, y2 = make_circles(n_samples=100, noise=0.05, shuffle=True, random_state=1)
X3, y3 = make_blobs(n_samples=500, centers=3, n_features=2,shuffle=True,
random_state=10)
fig, axs = plt.subplots(2,2)
axs[0, 0].plot(X0[:,0][y0==0],X0[:,1][y0==0],"ro", alpha=0.5)
axs[0, 0].plot(X0[:,0][y0==1],X0[:,1][y0==1],"bo", alpha=0.5)
# Dataset a moons
axs[0, 1].plot(X1[:,0][y1==0],X1[:,1][y1==0],"ro", alpha=0.5)
axs[0, 1].plot(X1[:,0][y1==1],X1[:,1][y1==1],"bo", alpha=0.5)
# Dataset circles
axs[1, 1].plot(X3[:,0][y3==0],X3[:,1][y3==0],"ro", alpha=0.5)
axs[1, 1].plot(X3[:,0][y3==1],X3[:,1][y3==1],"bo", alpha=0.5)
axs[1, 1].plot(X3[:,0][y3==2],X3[:,1][y3==2],"go", alpha=0.5)
[<matplotlib.lines.Line2D at 0x7f8a333191d0>]