Solución a un problema general de machine learning

Solución a un problema general de machine learning¶

En esta sesión se trabajará con las datos de los precios de las casas de california para dar solución a un problema real

Referencia: Basado del libro hand on machine learning y Kaggle

Generar una visión general del problema
Obtener los datos
Explorar los datos
Descubrir y visualizar los datos
Preparar los datos para un algoritmo de machinine learning
Selecccionar los modelos
Elegir el mejor modelo tuneando los parametros de ajuste
Presentar la solucion
Moniterar y analizar los datos.

https://www.kaggle.com/rahulallakonda/california-housing

Data.¶

Leer los datos
Analizar el estado de los datos
Limpiar los datos.
Analizar los datos.

import pandas as pd

# Read data
df.read_csv("")
df.read_excel(")

# Entender los datos
df.head()
df.info()
df.describe()
df["name_columns"].unique()
df.isnull().sum()
df.isnan().sum()
df.groupby(by=["name_cols"]).mean()
df.groupby(by=["name_cols"]).count()
df.groupby(by=["name_cols"]).sum()
df.hist()

import pandas as pd
import seaborn as sns
import matplotlib.pylab as plt
import numpy as np

#Si no recuerda los comandos de pandas, puede ver una cheat sheet 
#https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf

data_link = "https://raw.githubusercontent.com/hernansalinas/Curso_aprendizaje_estadistico/main/datasets/Sesion_07_housing.csv"
df = pd.read_csv(data_link)

df.head()

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0	NEAR BAY
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0	NEAR BAY
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0	NEAR BAY
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0	NEAR BAY
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0	NEAR BAY

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
 #   Column              Non-Null Count  Dtype  
---  ------              --------------  -----  
 0   longitude           20640 non-null  float64
 1   latitude            20640 non-null  float64
 2   housing_median_age  20640 non-null  float64
 3   total_rooms         20640 non-null  float64
 4   total_bedrooms      20433 non-null  float64
 5   population          20640 non-null  float64
 6   households          20640 non-null  float64
 7   median_income       20640 non-null  float64
 8   median_house_value  20640 non-null  float64
 9   ocean_proximity     20640 non-null  object 
dtypes: float64(9), object(1)
memory usage: 1.6+ MB

df.describe()

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
count	20640.000000	20640.000000	20640.000000	20640.000000	20433.000000	20640.000000	20640.000000	20640.000000	20640.000000
mean	-119.569704	35.631861	28.639486	2635.763081	537.870553	1425.476744	499.539680	3.870671	206855.816909
std	2.003532	2.135952	12.585558	2181.615252	421.385070	1132.462122	382.329753	1.899822	115395.615874
min	-124.350000	32.540000	1.000000	2.000000	1.000000	3.000000	1.000000	0.499900	14999.000000
25%	-121.800000	33.930000	18.000000	1447.750000	296.000000	787.000000	280.000000	2.563400	119600.000000
50%	-118.490000	34.260000	29.000000	2127.000000	435.000000	1166.000000	409.000000	3.534800	179700.000000
75%	-118.010000	37.710000	37.000000	3148.000000	647.000000	1725.000000	605.000000	4.743250	264725.000000
max	-114.310000	41.950000	52.000000	39320.000000	6445.000000	35682.000000	6082.000000	15.000100	500001.000000

df.isnull().sum()

longitude               0
latitude                0
housing_median_age      0
total_rooms             0
total_bedrooms        207
population              0
households              0
median_income           0
median_house_value      0
ocean_proximity         0
dtype: int64

df.isna().sum()

longitude               0
latitude                0
housing_median_age      0
total_rooms             0
total_bedrooms        207
population              0
households              0
median_income           0
median_house_value      0
ocean_proximity         0
dtype: int64

df["ocean_proximity"].unique()

array(['NEAR BAY', '<1H OCEAN', 'INLAND', 'NEAR OCEAN', 'ISLAND'],
      dtype=object)

cols = ["housing_median_age",	"total_rooms",	"total_bedrooms",	"population",	"households",	"median_income",	"median_house_value","ocean_proximity"]
df[cols].groupby(by=["ocean_proximity"]).mean()

	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
ocean_proximity
<1H OCEAN	29.279225	2628.343586	546.539185	1520.290499	517.744965	4.230682	240084.285464
INLAND	24.271867	2717.742787	533.881619	1391.046252	477.447565	3.208996	124805.392001
ISLAND	42.400000	1574.600000	420.400000	668.000000	276.600000	2.744420	380440.000000
NEAR BAY	37.730131	2493.589520	514.182819	1230.317467	488.616157	4.172885	259212.311790
NEAR OCEAN	29.347254	2583.700903	538.615677	1354.008653	501.244545	4.005785	249433.977427

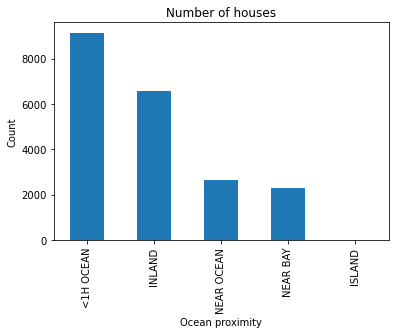
df.ocean_proximity.value_counts().plot(kind="bar")
plt.title('Number of houses')
plt.xlabel("Ocean proximity")
plt.ylabel('Count')
plt.show()

../_images/Sesion_07_Ejemplo_practico_13_0.png

df.hist(alpha=0.5, figsize=(10,8))

array([[<AxesSubplot:title={'center':'longitude'}>,
        <AxesSubplot:title={'center':'latitude'}>,
        <AxesSubplot:title={'center':'housing_median_age'}>],
       [<AxesSubplot:title={'center':'total_rooms'}>,
        <AxesSubplot:title={'center':'total_bedrooms'}>,
        <AxesSubplot:title={'center':'population'}>],
       [<AxesSubplot:title={'center':'households'}>,
        <AxesSubplot:title={'center':'median_income'}>,
        <AxesSubplot:title={'center':'median_house_value'}>]],
      dtype=object)

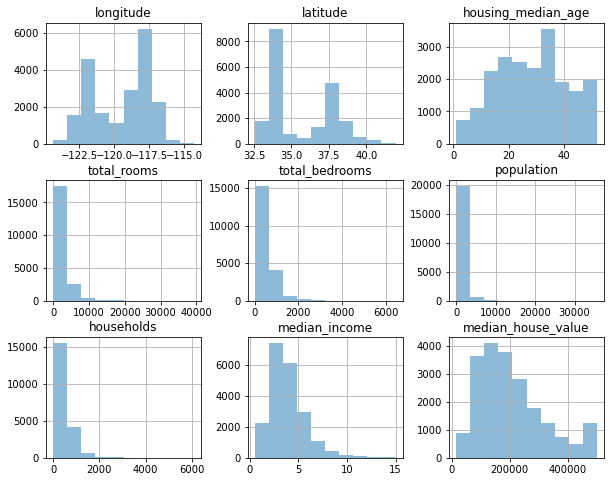
../_images/Sesion_07_Ejemplo_practico_14_1.png

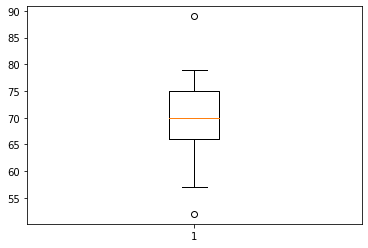
Diagrama de caja¶

Interpretación de un diagrama de caja¶

Desde el minimo al valor más bajo de la caja: primer cuartil, 25% de los datos
Desde el valor más bajo de la caja hasta la mediana: segundo cuartil, 25% de los datos
Desde la mediana hasta el valor mas alto de la caja : tercer cuartil, 25% de los datos
Desde el valor mas alto de la caja hasta el máximo: Cuarto cuartil, 25% de los datos

El rango intercuartil $IQR = Q_3-Q_1$ permite definir que datos pueden ser atipicos, basado en los siguientes limites:

$Max = Q3 + 1.5IQR$

$Min = Q1 - 1.5IQR$

Veamos un ejemplo:

T = np.array([52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89])
Tsort = np.sort(T)
print(f"T sort:{Tsort}")

IQR=9
max_ = 75 + 1.5*IQR
min_ = 66 - 1.5*IQR
print(max_)
print(min_)
plt.boxplot(T)

T sort:[52 57 57 58 63 66 66 67 67 68 69 70 70 70 70 72 73 75 75 76 76 78 79 89]
88.5
52.5

{'whiskers': [<matplotlib.lines.Line2D at 0x2190fdaff10>,
  <matplotlib.lines.Line2D at 0x2190fddc220>],
 'caps': [<matplotlib.lines.Line2D at 0x2190fddc5b0>,
  <matplotlib.lines.Line2D at 0x2190fddc7c0>],
 'boxes': [<matplotlib.lines.Line2D at 0x2190fdafc40>],
 'medians': [<matplotlib.lines.Line2D at 0x2190fddca90>],
 'fliers': [<matplotlib.lines.Line2D at 0x2190fddcd60>],
 'means': []}

../_images/Sesion_07_Ejemplo_practico_16_2.png

volviendo a nuestro datos tenemos que:

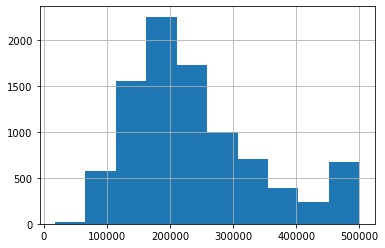
df2 = df[df["ocean_proximity"] == "<1H OCEAN"]
df2["median_house_value"].hist()

<AxesSubplot:>

../_images/Sesion_07_Ejemplo_practico_18_1.png

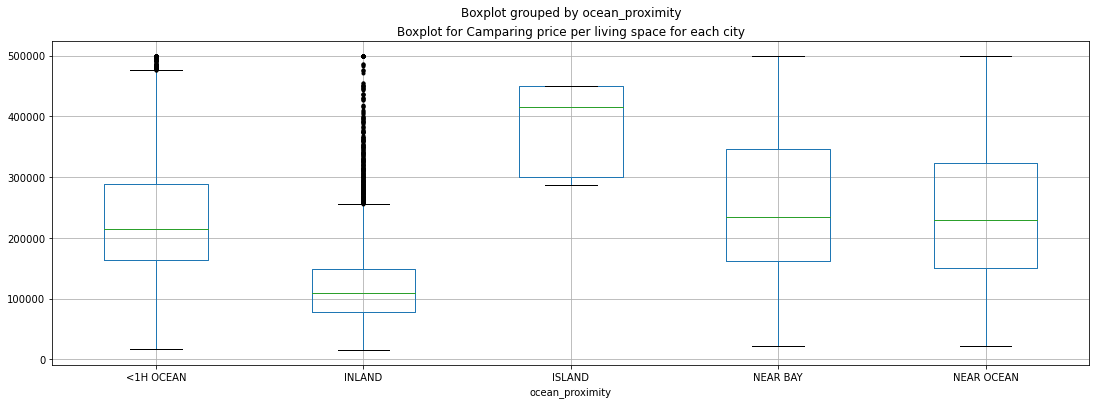
#draw boxplot
df.boxplot(column="median_house_value", by='ocean_proximity', sym = 'k.', figsize=(18,6))
#set title
plt.title('Boxplot for Camparing price per living space for each city')
plt.show()

../_images/Sesion_07_Ejemplo_practico_19_0.png

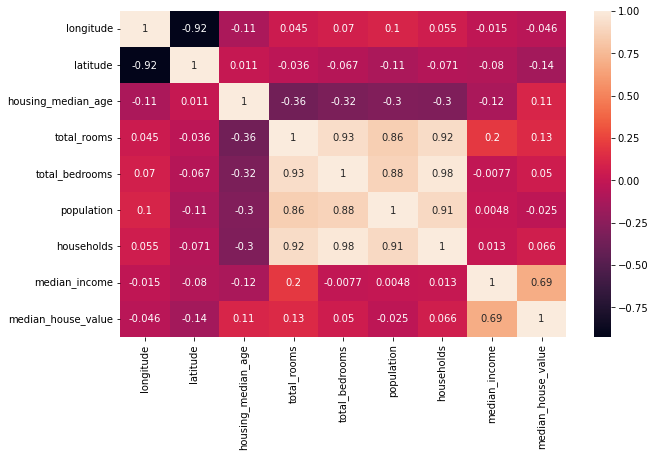
Matrix de correlación ¶

¿Como se determina la matrix de correlación?

corr_matrix = df.corr()
corr_matrix

plt.figure(figsize = (10,6))
sns.heatmap(corr_matrix, annot = True)
plt.show()

corr_matrix = df.corr()
corr_matrix

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
longitude	1.000000	-0.924664	-0.108197	0.044568	0.069608	0.099773	0.055310	-0.015176	-0.045967
latitude	-0.924664	1.000000	0.011173	-0.036100	-0.066983	-0.108785	-0.071035	-0.079809	-0.144160
housing_median_age	-0.108197	0.011173	1.000000	-0.361262	-0.320451	-0.296244	-0.302916	-0.119034	0.105623
total_rooms	0.044568	-0.036100	-0.361262	1.000000	0.930380	0.857126	0.918484	0.198050	0.134153
total_bedrooms	0.069608	-0.066983	-0.320451	0.930380	1.000000	0.877747	0.979728	-0.007723	0.049686
population	0.099773	-0.108785	-0.296244	0.857126	0.877747	1.000000	0.907222	0.004834	-0.024650
households	0.055310	-0.071035	-0.302916	0.918484	0.979728	0.907222	1.000000	0.013033	0.065843
median_income	-0.015176	-0.079809	-0.119034	0.198050	-0.007723	0.004834	0.013033	1.000000	0.688075
median_house_value	-0.045967	-0.144160	0.105623	0.134153	0.049686	-0.024650	0.065843	0.688075	1.000000

# Visualización de la matrix de correlación
plt.figure(figsize = (10,6))
sns.heatmap(corr_matrix, annot = True)
plt.show()

../_images/Sesion_07_Ejemplo_practico_22_0.png

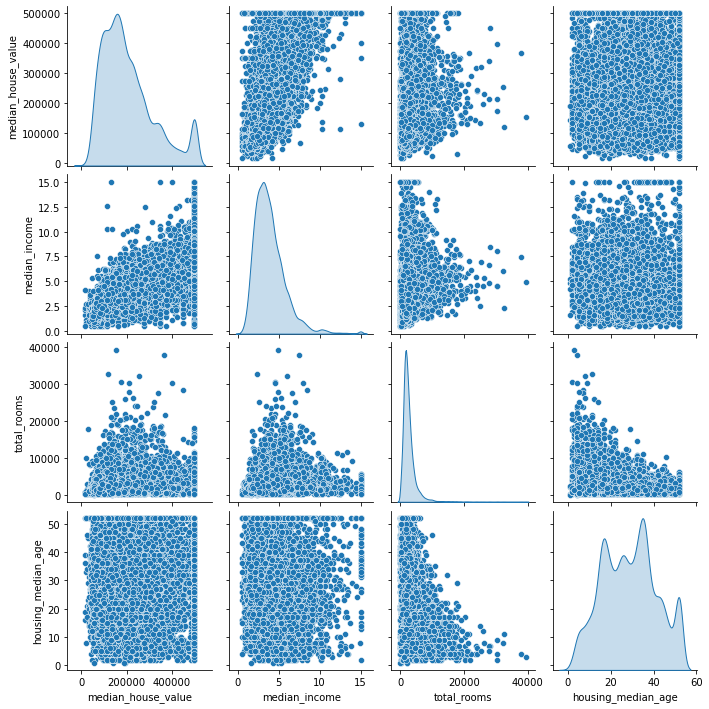
cols = ["median_house_value", "median_income", "total_rooms","housing_median_age"]
#pd.plotting.scatter_matrix(df[cols], alpha = 0.2, figsize = (12,8))
g = sns.pairplot(df[cols], diag_kind="kde")

../_images/Sesion_07_Ejemplo_practico_23_0.png

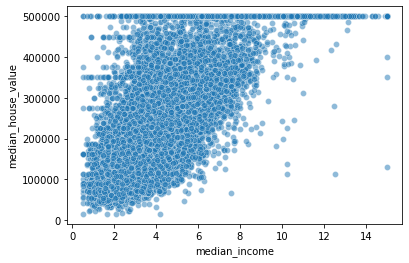
ax = sns.scatterplot(df.median_income, df.median_house_value, alpha = 0.5)

C:\Users\salin\anaconda3\envs\book\lib\site-packages\seaborn\_decorators.py:36: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
  warnings.warn(

../_images/Sesion_07_Ejemplo_practico_24_1.png

#sns.set()
#tips = sns.load_dataset("tips")

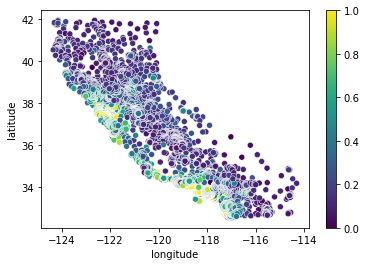
ax = sns.scatterplot(df.longitude,df.latitude, c=df.median_house_value)
sm = plt.cm.ScalarMappable()
ax.figure.colorbar(sm)

C:\Users\salin\anaconda3\envs\book\lib\site-packages\seaborn\_decorators.py:36: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
  warnings.warn(

<matplotlib.colorbar.Colorbar at 0x21911a07c10>

../_images/Sesion_07_Ejemplo_practico_25_2.png

# cols=df.columns
# cols
# fig, axs = plt.subplots(3, 3, figsize=(10,10))
# fig.add_gridspec(3, 3, hspace=10, wspace=40)
# k = 0
# for i in range(0,3):
#     for j in range(0,3):        
#         sns.histplot(df[cols[k]],ax=axs[i, j])
#         #sns.kdeplot(df[cols[k]], ax=axs[i, j],color="b")        
#         axs[i, j].legend(fontsize = 8)        
        
#         if(j==0):
#           axs[i, j].set_ylabel("")
#         if(i==2):
#           axs[i, j].set_xlabel("")
#         k=k+1

df

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0	NEAR BAY
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0	NEAR BAY
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0	NEAR BAY
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0	NEAR BAY
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0	NEAR BAY
...	...	...	...	...	...	...	...	...	...	...
20635	-121.09	39.48	25.0	1665.0	374.0	845.0	330.0	1.5603	78100.0	INLAND
20636	-121.21	39.49	18.0	697.0	150.0	356.0	114.0	2.5568	77100.0	INLAND
20637	-121.22	39.43	17.0	2254.0	485.0	1007.0	433.0	1.7000	92300.0	INLAND
20638	-121.32	39.43	18.0	1860.0	409.0	741.0	349.0	1.8672	84700.0	INLAND
20639	-121.24	39.37	16.0	2785.0	616.0	1387.0	530.0	2.3886	89400.0	INLAND

20640 rows × 10 columns

# Combinar caracteristics puede ser una buena forma de definir nuevas variables y mejorar
# los entrenamientos del algoritmo.

Preparación de data para un algoritmo de machine learning¶

Evitar el data Snooping bias.¶

En algunos casos se sugiere dividir los datos en entrenamiento y test desde el principio dado que el cerebro puede sobreajustar el dataset y los resultados no significativos se pueden volver significativos. El procedimiento correcto es probar cualquier hipótesis en un conjunto de datos que no se utilizó para generar la hipótesis.

Sampling bias¶

Si el dataset es lo suficientemente grande un muestreo aleatorio de la muestra puede ser considerado, sin embargo si la muestra es pequena se debe garantizar homegeniedad en el dataset de entrenamiento.

Ejemplo:

Por ejemplo, la población de EE. UU. esta compuesto por un 51,3 % de mujeres y un 48,7 % de hombres, por lo que una encuesta bien realizada en EEUU trata de mantener esta proporción en la muestra: 513 mujeres y 487 hombres. Esto se llama muestreo estratificado(stratified sampling): la población se divide en subgrupos homogéneos llamados estratos(strata), y se muestrea el número correcto de instancias de cada estrato para garantizar que el El conjunto de prueba es representativo de la población general. Si usaran muestras puramente aleatorias, habría alrededor del 12% de posibilidades de muestrear un conjunto de prueba sesgado con menos del 49% de mujeres o más del 54% de mujeres. De cualquier manera, los resultados de la encuesta serían significativamente sesgada.

# https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html
from sklearn.model_selection import train_test_split

# ¿Es significativa la muestra que se esta considerando?
train_set, test_set \
  = train_test_split(df, test_size = 0.2, random_state = 42)

print(len(train_set))
print(len(test_set))

16512
4128

df

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0	NEAR BAY
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0	NEAR BAY
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0	NEAR BAY
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0	NEAR BAY
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0	NEAR BAY
...	...	...	...	...	...	...	...	...	...	...
20635	-121.09	39.48	25.0	1665.0	374.0	845.0	330.0	1.5603	78100.0	INLAND
20636	-121.21	39.49	18.0	697.0	150.0	356.0	114.0	2.5568	77100.0	INLAND
20637	-121.22	39.43	17.0	2254.0	485.0	1007.0	433.0	1.7000	92300.0	INLAND
20638	-121.32	39.43	18.0	1860.0	409.0	741.0	349.0	1.8672	84700.0	INLAND
20639	-121.24	39.37	16.0	2785.0	616.0	1387.0	530.0	2.3886	89400.0	INLAND

20640 rows × 10 columns

División del dataset en grupos¶

La siguiente division debe ser basada en la experticie de lo que se esta realizando, y sobre ello se debe tomar una muestra significativa

df["income_cat"] = pd.cut(df["median_income"],
                               bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
                               labels=[1, 2, 3, 4, 5])

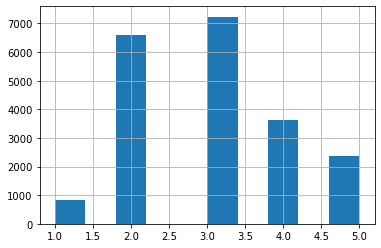
df.income_cat.hist()

<AxesSubplot:>

../_images/Sesion_07_Ejemplo_practico_37_1.png

from sklearn.model_selection import StratifiedShuffleSplit

split = StratifiedShuffleSplit(n_splits = 1, test_size=0.2, random_state=42)

for train_index, test_index in split.split(df, df["income_cat"]):
  strat_train_set = df.loc[train_index]
  strat_test_set = df.loc[test_index]

Proporciones del dataset¶

df["income_cat"].value_counts() / len(df)

  0.350581
  0.318847
  0.176308
  0.114438
  0.039826
Name: income_cat, dtype: float64

strat_train_set["income_cat"].value_counts() / len(strat_train_set)

  0.350594
  0.318859
  0.176296
  0.114462
  0.039789
Name: income_cat, dtype: float64

strat_test_set["income_cat"].value_counts() / len(strat_test_set)

  0.350533
  0.318798
  0.176357
  0.114341
  0.039971
Name: income_cat, dtype: float64

train_set, test_set \
  = train_test_split(df, test_size = 0.2, random_state = 42)

test_set["income_cat"].value_counts() / len(test_set)

  0.358527
  0.324370
  0.167393
  0.109496
  0.040213
Name: income_cat, dtype: float64

test_set["income_cat"].value_counts() / len(test_set)

  0.358527
  0.324370
  0.167393
  0.109496
  0.040213
Name: income_cat, dtype: float64

def income_cat_proportions(data):
    return data["income_cat"].value_counts() / len(data)

train_set, test_set = train_test_split(df, test_size = 0.2, random_state = 42)

compare_props = pd.DataFrame({
    "Overall": income_cat_proportions(df),
    "Stratified": income_cat_proportions(strat_test_set),
    "Random": income_cat_proportions(test_set),
}).sort_index()
compare_props["Rand. %error"] =abs( 100 * compare_props["Random"] / compare_props["Overall"] - 100)
compare_props["Strat. %error"] =abs( 100 * compare_props["Stratified"] / compare_props["Overall"] - 100)

compare_props

	Overall	Stratified	Random	Rand. %error	Strat. %error
1	0.039826	0.039971	0.040213	0.973236	0.364964
2	0.318847	0.318798	0.324370	1.732260	0.015195
3	0.350581	0.350533	0.358527	2.266446	0.013820
4	0.176308	0.176357	0.167393	5.056334	0.027480
5	0.114438	0.114341	0.109496	4.318374	0.084674

En Conclusion

#Si no recuerda los comandos de pandas, puede ver una cheat sheet 
#https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf
data_link = "https://raw.githubusercontent.com/hernansalinas/Curso_aprendizaje_estadistico/main/datasets/Sesion_07_housing.csv"
df = pd.read_csv(data_link)

#1. Leer los data. 
#2. Para hacer el split analizar si la muestra es significativa para el entrenamiento y test
#3. Dejar los data de test ocultos para hacer las pruebas

df["income_cat"] = pd.cut(df["median_income"],
                               bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
                               labels=[1, 2, 3, 4, 5])

split = StratifiedShuffleSplit(n_splits = 1, test_size=0.2, random_state=42)

for train_index, test_index in split.split(df, df["income_cat"]):
  strat_train_set = df.loc[train_index]
  strat_test_set = df.loc[test_index]

df_train = strat_train_set
df_test = strat_test_set

Matrix de correlación¶

corr_matrix = df_train.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)

median_house_value    1.000000
median_income         0.687151
total_rooms           0.135140
housing_median_age    0.114146
households            0.064590
total_bedrooms        0.047781
population           -0.026882
longitude            -0.047466
latitude             -0.142673
Name: median_house_value, dtype: float64

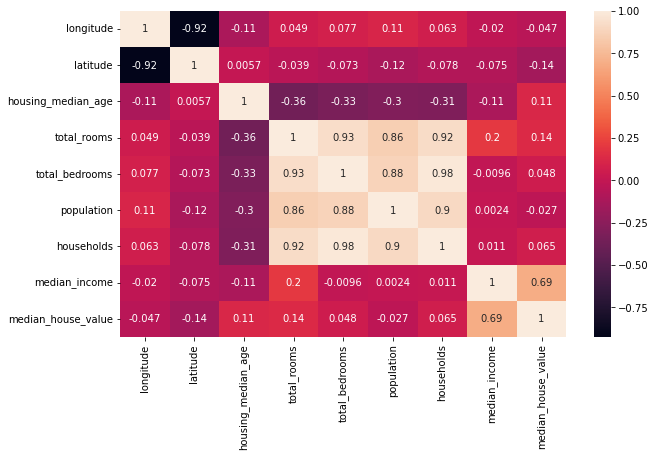
# Visualización de la matrix de correlación
plt.figure(figsize = (10,6))
sns.heatmap(corr_matrix, annot = True)
plt.show()

../_images/Sesion_07_Ejemplo_practico_54_0.png

Agregar nuevas variables¶

df_train["rooms_per_household"] = df_train["total_rooms"]/df_train["households"]
df_train["bedrooms_per_room"] = df_train["total_bedrooms"]/df_train["total_rooms"]
df_train["population_per_household"]=df_train["population"]/df_train["households"]

corr_matrix = df_train.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)

median_house_value          1.000000
median_income               0.687151
rooms_per_household         0.146255
total_rooms                 0.135140
housing_median_age          0.114146
households                  0.064590
total_bedrooms              0.047781
population_per_household   -0.021991
population                 -0.026882
longitude                  -0.047466
latitude                   -0.142673
bedrooms_per_room          -0.259952
Name: median_house_value, dtype: float64

# Visualización de la matrix de correlación
plt.figure(figsize = (10,6))
sns.heatmap(corr_matrix, annot = True)
plt.show()

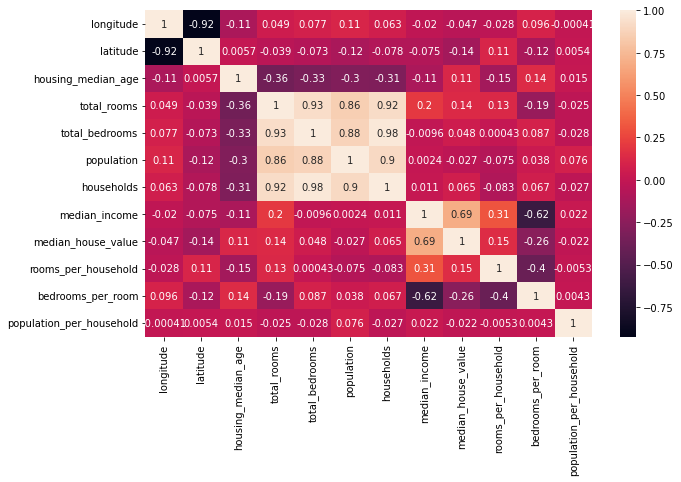
../_images/Sesion_07_Ejemplo_practico_58_0.png

Limpieza de datos¶

df_train.isnull().sum()

longitude                     0
latitude                      0
housing_median_age            0
total_rooms                   0
total_bedrooms              158
population                    0
households                    0
median_income                 0
median_house_value            0
ocean_proximity               0
income_cat                    0
rooms_per_household           0
bedrooms_per_room           158
population_per_household      0
dtype: int64

#df_train.dropna(subset=["total_bedrooms"]) #Eliminar los nan
#df_train.drop("total_bedrooms", axis=1)  # Eliminar la columna
median = df_train["total_bedrooms"].median()
q=df_train["total_bedrooms"].fillna(median).copy()

q=pd.DataFrame(q)

q.isnull().sum()

total_bedrooms    0
dtype: int64

Imputer¶

df_train_num = df_train.drop("ocean_proximity", axis=1)

from sklearn.impute import SimpleImputer
#imputer = Imputer(strategy="median")
imp_mean = SimpleImputer( strategy='mean')

imp_mean.fit(df_train_num)

SimpleImputer()

imp_mean.statistics_

array([-1.19575635e+02,  3.56393144e+01,  2.86534036e+01,  2.62253979e+03,
        5.34914639e+02,  1.41968738e+03,  4.97011810e+02,  3.87588428e+00,
        2.07005322e+05,  3.00678295e+00,  5.44040595e+00,  2.12872772e-01,
        3.09646921e+00])

df_train_num.median().values

C:\Users\salin\AppData\Local\Temp\ipykernel_3432\1957487952.py:1: FutureWarning: Dropping of nuisance columns in DataFrame reductions (with 'numeric_only=None') is deprecated; in a future version this will raise TypeError.  Select only valid columns before calling the reduction.
  df_train_num.median().values

array([-1.18510000e+02,  3.42600000e+01,  2.90000000e+01,  2.11900000e+03,
        4.33000000e+02,  1.16400000e+03,  4.08000000e+02,  3.54155000e+00,
        1.79500000e+05,  5.23234164e+00,  2.03027043e-01,  2.81766108e+00])

X = imp_mean.transform(df_train_num)

array([[-121.46      ,   38.52      ,   29.        , ...,    5.48583569,
           0.20578363,    3.16855524],
       [-117.23      ,   33.09      ,    7.        , ...,    6.92708333,
           0.16071429,    2.62369792],
       [-119.04      ,   35.37      ,   44.        , ...,    5.39333333,
           0.19159456,    2.22333333],
       ...,
       [-122.72      ,   38.44      ,   48.        , ...,    4.11046512,
           0.23479491,    2.6627907 ],
       [-122.7       ,   38.31      ,   14.        , ...,    6.29740519,
           0.18383518,    2.41117764],
       [-122.14      ,   39.97      ,   27.        , ...,    5.47715736,
           0.20574606,    3.17258883]])

housing_tr = pd.DataFrame(X, columns=df_train_num.columns)

housing_tr

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	income_cat	rooms_per_household	bedrooms_per_room	population_per_household
0	-121.46	38.52	29.0	3873.0	797.0	2237.0	706.0	2.1736	72100.0	2.0	5.485836	0.205784	3.168555
1	-117.23	33.09	7.0	5320.0	855.0	2015.0	768.0	6.3373	279600.0	5.0	6.927083	0.160714	2.623698
2	-119.04	35.37	44.0	1618.0	310.0	667.0	300.0	2.8750	82700.0	2.0	5.393333	0.191595	2.223333
3	-117.13	32.75	24.0	1877.0	519.0	898.0	483.0	2.2264	112500.0	2.0	3.886128	0.276505	1.859213
4	-118.70	34.28	27.0	3536.0	646.0	1837.0	580.0	4.4964	238300.0	3.0	6.096552	0.182692	3.167241
...	...	...	...	...	...	...	...	...	...	...	...	...	...
16507	-117.07	33.03	14.0	6665.0	1231.0	2026.0	1001.0	5.0900	268500.0	4.0	6.658342	0.184696	2.023976
16508	-121.42	38.51	15.0	7901.0	1422.0	4769.0	1418.0	2.8139	90400.0	2.0	5.571932	0.179977	3.363188
16509	-122.72	38.44	48.0	707.0	166.0	458.0	172.0	3.1797	140400.0	3.0	4.110465	0.234795	2.662791
16510	-122.70	38.31	14.0	3155.0	580.0	1208.0	501.0	4.1964	258100.0	3.0	6.297405	0.183835	2.411178
16511	-122.14	39.97	27.0	1079.0	222.0	625.0	197.0	3.1319	62700.0	3.0	5.477157	0.205746	3.172589

16512 rows × 13 columns

Manejo de texto y atributos categoricos¶

#from sklearn.preprocessing import OrdinalEncoder
from sklearn.preprocessing import OneHotEncoder

df_train["ocean_proximity"].unique()

array(['INLAND', 'NEAR OCEAN', '<1H OCEAN', 'NEAR BAY', 'ISLAND'],
      dtype=object)

housing_cat=df_train[["ocean_proximity"]]
housing_cat

	ocean_proximity
12655	INLAND
15502	NEAR OCEAN
2908	INLAND
14053	NEAR OCEAN
20496	<1H OCEAN
...	...
15174	<1H OCEAN
12661	INLAND
19263	<1H OCEAN
19140	<1H OCEAN
19773	INLAND

16512 rows × 1 columns

cat_encoder = OneHotEncoder(sparse=False)
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
print(housing_cat_1hot)
print(cat_encoder.categories_)

[[0. 1. 0. 0. 0.]
 [0. 0. 0. 0. 1.]
 [0. 1. 0. 0. 0.]
 ...
 [1. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]]
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
      dtype=object)]

Resumen de las transformaciones paso a paso¶

# Read Data
data_link = "https://raw.githubusercontent.com/hernansalinas/Curso_aprendizaje_estadistico/main/datasets/Sesion_07_housing.csv"
df = pd.read_csv(data_link)

# 1. Clasification 
df["income_cat"] = pd.cut(df["median_income"],
                               bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
                               labels=[1, 2, 3, 4, 5])

df_ = df.copy()


split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(df_, df_["income_cat"]):
 strat_train_set = df_.loc[train_index]
 strat_test_set = df_.loc[test_index]

for set in (strat_train_set, strat_test_set):
 set.drop(["income_cat"], axis=1, inplace=True)

strat_train_set

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity
12655	-121.46	38.52	29.0	3873.0	797.0	2237.0	706.0	2.1736	72100.0	INLAND
15502	-117.23	33.09	7.0	5320.0	855.0	2015.0	768.0	6.3373	279600.0	NEAR OCEAN
2908	-119.04	35.37	44.0	1618.0	310.0	667.0	300.0	2.8750	82700.0	INLAND
14053	-117.13	32.75	24.0	1877.0	519.0	898.0	483.0	2.2264	112500.0	NEAR OCEAN
20496	-118.70	34.28	27.0	3536.0	646.0	1837.0	580.0	4.4964	238300.0	<1H OCEAN
...	...	...	...	...	...	...	...	...	...	...
15174	-117.07	33.03	14.0	6665.0	1231.0	2026.0	1001.0	5.0900	268500.0	<1H OCEAN
12661	-121.42	38.51	15.0	7901.0	1422.0	4769.0	1418.0	2.8139	90400.0	INLAND
19263	-122.72	38.44	48.0	707.0	166.0	458.0	172.0	3.1797	140400.0	<1H OCEAN
19140	-122.70	38.31	14.0	3155.0	580.0	1208.0	501.0	4.1964	258100.0	<1H OCEAN
19773	-122.14	39.97	27.0	1079.0	222.0	625.0	197.0	3.1319	62700.0	INLAND

16512 rows × 10 columns

# 2 Add New variables to data
housing = strat_train_set.copy()
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]

housing

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity	rooms_per_household	bedrooms_per_room	population_per_household
12655	-121.46	38.52	29.0	3873.0	797.0	2237.0	706.0	2.1736	72100.0	INLAND	5.485836	0.205784	3.168555
15502	-117.23	33.09	7.0	5320.0	855.0	2015.0	768.0	6.3373	279600.0	NEAR OCEAN	6.927083	0.160714	2.623698
2908	-119.04	35.37	44.0	1618.0	310.0	667.0	300.0	2.8750	82700.0	INLAND	5.393333	0.191595	2.223333
14053	-117.13	32.75	24.0	1877.0	519.0	898.0	483.0	2.2264	112500.0	NEAR OCEAN	3.886128	0.276505	1.859213
20496	-118.70	34.28	27.0	3536.0	646.0	1837.0	580.0	4.4964	238300.0	<1H OCEAN	6.096552	0.182692	3.167241
...	...	...	...	...	...	...	...	...	...	...	...	...	...
15174	-117.07	33.03	14.0	6665.0	1231.0	2026.0	1001.0	5.0900	268500.0	<1H OCEAN	6.658342	0.184696	2.023976
12661	-121.42	38.51	15.0	7901.0	1422.0	4769.0	1418.0	2.8139	90400.0	INLAND	5.571932	0.179977	3.363188
19263	-122.72	38.44	48.0	707.0	166.0	458.0	172.0	3.1797	140400.0	<1H OCEAN	4.110465	0.234795	2.662791
19140	-122.70	38.31	14.0	3155.0	580.0	1208.0	501.0	4.1964	258100.0	<1H OCEAN	6.297405	0.183835	2.411178
19773	-122.14	39.97	27.0	1079.0	222.0	625.0	197.0	3.1319	62700.0	INLAND	5.477157	0.205746	3.172589

16512 rows × 13 columns

housing_labels = housing["median_house_value"].copy()
housing = housing.drop("median_house_value", axis=1)

housing.isnull().sum()

longitude                     0
latitude                      0
housing_median_age            0
total_rooms                   0
total_bedrooms              158
population                    0
households                    0
median_income                 0
ocean_proximity               0
rooms_per_household           0
bedrooms_per_room           158
population_per_household      0
dtype: int64

housing_num = housing.drop("ocean_proximity", axis=1)
housing_num

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	rooms_per_household	bedrooms_per_room	population_per_household
12655	-121.46	38.52	29.0	3873.0	797.0	2237.0	706.0	2.1736	5.485836	0.205784	3.168555
15502	-117.23	33.09	7.0	5320.0	855.0	2015.0	768.0	6.3373	6.927083	0.160714	2.623698
2908	-119.04	35.37	44.0	1618.0	310.0	667.0	300.0	2.8750	5.393333	0.191595	2.223333
14053	-117.13	32.75	24.0	1877.0	519.0	898.0	483.0	2.2264	3.886128	0.276505	1.859213
20496	-118.70	34.28	27.0	3536.0	646.0	1837.0	580.0	4.4964	6.096552	0.182692	3.167241
...	...	...	...	...	...	...	...	...	...	...	...
15174	-117.07	33.03	14.0	6665.0	1231.0	2026.0	1001.0	5.0900	6.658342	0.184696	2.023976
12661	-121.42	38.51	15.0	7901.0	1422.0	4769.0	1418.0	2.8139	5.571932	0.179977	3.363188
19263	-122.72	38.44	48.0	707.0	166.0	458.0	172.0	3.1797	4.110465	0.234795	2.662791
19140	-122.70	38.31	14.0	3155.0	580.0	1208.0	501.0	4.1964	6.297405	0.183835	2.411178
19773	-122.14	39.97	27.0	1079.0	222.0	625.0	197.0	3.1319	5.477157	0.205746	3.172589

16512 rows × 11 columns

# Imputer
imp_mean = SimpleImputer( strategy='mean')
imp_mean.fit(housing_num)
imp_mean.statistics_

array([-1.19575635e+02,  3.56393144e+01,  2.86534036e+01,  2.62253979e+03,
        5.34914639e+02,  1.41968738e+03,  4.97011810e+02,  3.87588428e+00,
        5.44040595e+00,  2.12872772e-01,  3.09646921e+00])

X = imp_mean.transform(housing_num)
housing_tr = pd.DataFrame(X, columns = housing_num.columns)

housing_tr.isnull().sum()

longitude                   0
latitude                    0
housing_median_age          0
total_rooms                 0
total_bedrooms              0
population                  0
households                  0
median_income               0
rooms_per_household         0
bedrooms_per_room           0
population_per_household    0
dtype: int64

# 3. One hot encoder
housing_cat = housing[["ocean_proximity"]]
cat_encoder = OneHotEncoder(sparse=False)
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
print(housing_cat_1hot)
print(cat_encoder.categories_)

[[0. 1. 0. 0. 0.]
 [0. 0. 0. 0. 1.]
 [0. 1. 0. 0. 0.]
 ...
 [1. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]]
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
      dtype=object)]

housing_cat_1hot

array([[0., 1., 0., 0., 0.],
       [0., 0., 0., 0., 1.],
       [0., 1., 0., 0., 0.],
       ...,
       [1., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.]])

cat_encoder.categories_[0]

array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
      dtype=object)

df_cat_1hot = pd.DataFrame(housing_cat_1hot, columns = cat_encoder.categories_[0])

df_cat_1hot

	<1H OCEAN	INLAND	ISLAND	NEAR BAY	NEAR OCEAN
0	0.0	1.0	0.0	0.0	0.0
1	0.0	0.0	0.0	0.0	1.0
2	0.0	1.0	0.0	0.0	0.0
3	0.0	0.0	0.0	0.0	1.0
4	1.0	0.0	0.0	0.0	0.0
...	...	...	...	...	...
16507	1.0	0.0	0.0	0.0	0.0
16508	0.0	1.0	0.0	0.0	0.0
16509	1.0	0.0	0.0	0.0	0.0
16510	1.0	0.0	0.0	0.0	0.0
16511	0.0	1.0	0.0	0.0	0.0

16512 rows × 5 columns

housing_tr_ = housing_tr.join(df_cat_1hot)

Escalamiento de variables¶

cols=["longitude", "latitude",	"housing_median_age",	"total_rooms",\
      "total_bedrooms",	"population",	"households",	"median_income",\
      "<1H OCEAN",	"INLAND",	"ISLAND",	"NEAR BAY", "NEAR OCEAN"]

housing_scale=housing_tr_[cols]

housing_scale

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	<1H OCEAN	INLAND	ISLAND	NEAR BAY	NEAR OCEAN
0	-121.46	38.52	29.0	3873.0	797.0	2237.0	706.0	2.1736	0.0	1.0	0.0	0.0	0.0
1	-117.23	33.09	7.0	5320.0	855.0	2015.0	768.0	6.3373	0.0	0.0	0.0	0.0	1.0
2	-119.04	35.37	44.0	1618.0	310.0	667.0	300.0	2.8750	0.0	1.0	0.0	0.0	0.0
3	-117.13	32.75	24.0	1877.0	519.0	898.0	483.0	2.2264	0.0	0.0	0.0	0.0	1.0
4	-118.70	34.28	27.0	3536.0	646.0	1837.0	580.0	4.4964	1.0	0.0	0.0	0.0	0.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...
16507	-117.07	33.03	14.0	6665.0	1231.0	2026.0	1001.0	5.0900	1.0	0.0	0.0	0.0	0.0
16508	-121.42	38.51	15.0	7901.0	1422.0	4769.0	1418.0	2.8139	0.0	1.0	0.0	0.0	0.0
16509	-122.72	38.44	48.0	707.0	166.0	458.0	172.0	3.1797	1.0	0.0	0.0	0.0	0.0
16510	-122.70	38.31	14.0	3155.0	580.0	1208.0	501.0	4.1964	1.0	0.0	0.0	0.0	0.0
16511	-122.14	39.97	27.0	1079.0	222.0	625.0	197.0	3.1319	0.0	1.0	0.0	0.0	0.0

16512 rows × 13 columns

from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
scaler.fit(housing_scale)

MinMaxScaler()

X = scaler.transform(housing_scale)
X

array([[0.28784861, 0.63549416, 0.54901961, ..., 0.        , 0.        ,
        0.        ],
       [0.70916335, 0.05844846, 0.11764706, ..., 0.        , 0.        ,
        1.        ],
       [0.52888446, 0.30074389, 0.84313725, ..., 0.        , 0.        ,
        0.        ],
       ...,
       [0.1623506 , 0.62699256, 0.92156863, ..., 0.        , 0.        ,
        0.        ],
       [0.16434263, 0.61317747, 0.25490196, ..., 0.        , 0.        ,
        0.        ],
       [0.22011952, 0.78958555, 0.50980392, ..., 0.        , 0.        ,
        0.        ]])

housing_prepared = pd.DataFrame(X, columns = housing_scale.columns)

len(housing_prepared)

len(housing_labels)

# Consideremos las siguientes columnas: 
cols=["longitude", "latitude",	"housing_median_age",	"total_rooms",\
      "total_bedrooms",	"population",	"households",	"median_income"]
housing_prep = housing_prepared[cols]

housing_prep

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income
0	0.287849	0.635494	0.549020	0.098362	0.128061	0.062614	0.131441	0.115426
1	0.709163	0.058448	0.117647	0.135168	0.137403	0.056392	0.143017	0.402574
2	0.528884	0.300744	0.843137	0.041003	0.049613	0.018610	0.055639	0.163798
3	0.719124	0.022317	0.450980	0.047591	0.083280	0.025085	0.089806	0.119067
4	0.562749	0.184910	0.509804	0.089790	0.103737	0.051403	0.107916	0.275617
...	...	...	...	...	...	...	...	...
16507	0.725100	0.052072	0.254902	0.169380	0.197970	0.056700	0.186520	0.316554
16508	0.291833	0.634431	0.274510	0.200819	0.228737	0.133580	0.264376	0.159584
16509	0.162351	0.626993	0.921569	0.017831	0.026418	0.012753	0.031740	0.184811
16510	0.164343	0.613177	0.254902	0.080099	0.093106	0.033773	0.093167	0.254928
16511	0.220120	0.789586	0.509804	0.027293	0.035438	0.017433	0.036408	0.181515

16512 rows × 8 columns

from sklearn.linear_model import LinearRegression

model = LinearRegression()
model.fit(housing_prep, housing_labels)
housing_predictions = model.predict(housing_prep)

model.score(housing_prep, housing_labels)

0.6343991933140793

#¿Como autmatizar todo el proceso?
#¿El modelo de regresion lineal es valido para lo construido, 
#que informacion nos da el score?
#¿Se puede mejorar agregando nuevas caracteristicas?
# ¿Puede ser ajustado a otro modelo?

Regresion multivariada ecuacion normal, repaso breve.

Regresión Logística

Aprendizaje Estatadistico

Solución a un problema general de machine learning

Contents

Solución a un problema general de machine learning¶

Data.¶

Diagrama de caja ¶

Diagrama de caja¶

Interpretación de un diagrama de caja¶

Matrix de correlación ¶

Preparación de data para un algoritmo de machine learning¶

Evitar el data Snooping bias.¶

Sampling bias¶

División del dataset en grupos¶

Proporciones del dataset¶

Matrix de correlación¶

Agregar nuevas variables¶

Limpieza de datos¶

Imputer¶

Manejo de texto y atributos categoricos¶

Resumen de las transformaciones paso a paso¶

Escalamiento de variables¶