Regresión Logística
Contents
Regresión Logística¶
Si deseamos clasificar algún tipo de imagen, resultado en campos medicos, astrofisicos se pueden aplicar algoritmos de clasificación. En particular en esta sesión se estudia los principios basicos de regresión logística para aplicarla a los modelos de clasificación.
Supongamos que queremos clasificar dos tipos, basado en dos características:
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification,make_circles
import numpy as np
X1, Y1 = make_classification(
n_features = 2, n_redundant = 0, n_informative=1, n_clusters_per_class=1,
random_state = 1, class_sep=1.2, flip_y = 0.15)
plt.figure()
plt.scatter(X1[:, 0], X1[:, 1], marker="o", c=Y1, s=25, edgecolor="k")
plt.xlabel("X_1")
plt.ylabel("X_2")
Text(0, 0.5, 'X_2')
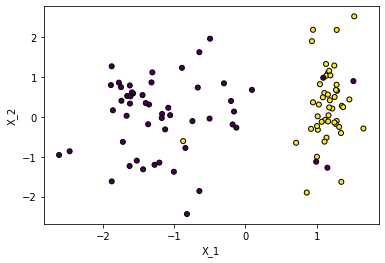
En este caso cada color representa los objetos tipos 0 y tipo 1. Para aplicar un algoritmo de clasificación relacionaremos el valor $h_{\theta}(X^{i})$ con la probabilidad de obtener un valor de y dado un x parametrizado por $\theta$, $P(y|x;\theta)$, asi :
$h_{\theta}(X^{i}) = P(y|x;\theta) $
Se cumple que: $P(y=1|x;\theta)+P(y=0|x;\theta) = 1$
Si tenemos muestra equiprobables, podemos definir lo siguiente para P :
$P<0.5$ se obtienen los objetos tipo 0
$P \geq 0.5$ se obtienen los objetos tipo 1
Podemos establecer un clasificador de lods sistemas basado en las probabilidades a partir de un clasificador logístico:
Cuya derivada es :
f = lambda x: 1/(1+np.exp(-x))
fp = lambda x: f(x)*(1-f(x))
z=np.linspace(-10, 10, 100)
plt.figure()
plt.plot(z,f(z), label="f(z)")
plt.plot(z,fp(z), label="Derivada de f(z)")
plt.ylabel("f(z)")
plt.xlabel("z")
plt.grid()
plt.legend()
<matplotlib.legend.Legend at 0x210bd69f220>
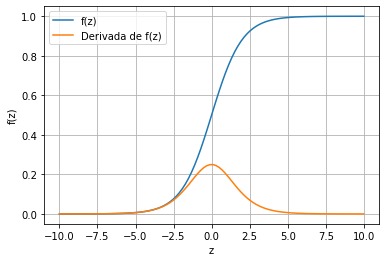
Para valores de $z< 0.0$ la regresión logistica clasica objetos tipo 0, siendo $f(z)<0.5$
Para valores de $z\geq 0.0$ la regresión logística clasica objetos tipo 1 siendo $f(z) \geq 0.5$
¿Cual es la probabilidad de que dado un hyperplano, los valores de un hyperlado sean objetos tipo 0 o tipo 1?
Aplicando la regresión logistica, a las regresiones multivariadas estudiadas en la sesiones anteriores, tenemos que el argumento $z=\Theta^{T} X$, así:
Se cumple que para los valores del hyperplano $\Theta^T X\geq 0.0$, $y = 1$
Se cumple que para $\Theta^T X < 0.0$ , $y = 0$
Las condiciones anteriores permiten definir fronteras de desicion entre los datos a clasificar. Para los datos dados arriba, se puede establecer el siguiente clasificador.
$h_\theta(x) = g(\theta_0+\theta_1 x_1+\theta_2 x_2 ) $.
Una clasificación del dataset nos sugiere que la frontera para este dataset es:
$\theta_0+\theta_1 x_1+\theta_2 x_2 \geq 0.0$
Si por algun metodo encontramos que los parametros $\Theta$ entonces podemos definir la frontera de clasifiación. Como ejemplo supongamos que encontramos los siguientes parametros $\Theta=[3.0, -20, 1.0]$
Ecnontrar la ecuacion de la recta y mejorar la parametrizacion
$3-20x1+x2=0$
$x_2= 20 x_1 - 3$
x1 = np.linspace(0, 0.29, 100)
x2 = 20*x1-3
X1, Y1 = make_classification(
n_features = 2, n_redundant = 0, n_informative=1, n_clusters_per_class=1,
random_state = 1, class_sep=1.2, flip_y = 0.15)
plt.figure()
plt.scatter(X1[:, 0], X1[:, 1], marker="o", c=Y1, s=25, edgecolor="k")
plt.plot(x1, x2)
plt.xlabel("X_1")
plt.ylabel("X_2")
Text(0, 0.5, 'X_2')
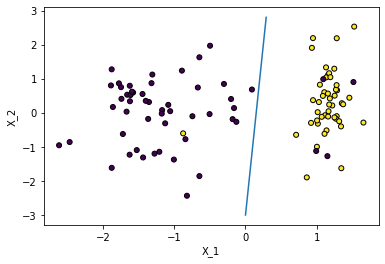
Fronteras no lineal también puede ser consideradas, para ello se puede definir $\Theta^T X$ como funcion de un polinomio, por ejemplo
$\Theta^T X = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 +\theta_4 x_1^4$
La frontera de desición en este caso esta determinada por:
$\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 +\theta_4 x_1^4 \geq 0$ para obtener un clasificador con valores de y = 1.
Para este mismo caso, supongamos que tenmos la siguiente distribución de datos, ¿Cuál es el mejor elección de parámetros $\Theta$ que permite clasificar los datos siguientes:
X, y = make_circles(
n_samples=100, factor=0.5, noise=0.05, random_state=0)
red = y == 0
green = y == 1
f, ax = plt.subplots()
ax.scatter(X[red, 0], X[red, 1], c="r")
ax.scatter(X[green, 0], X[green, 1], c="g")
plt.axis("tight")
(-1.12244940477901, 1.1839643638442499, -1.2696420440360447, 1.185918477713659)
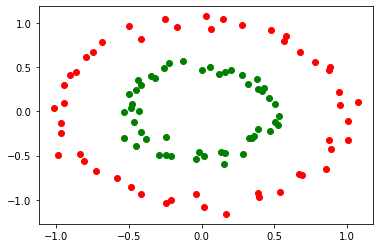
Analizando el conjunto de datos, se puede observar que la frontera es la de una circunferencia con centro en (0, 0) y radio de 0.7 aproxidamente, asi nuestra elección de parámetros para el polinomio ejemplicado en la celda anterior ($\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 +\theta_4 x_1^4 \geq 0$ ) es:
$\Theta^T = [0.7,0, 0, 1,1 ] $
Reemplando tenemos que:
$-0.7+x_1^2+x_2^2 \geq 0$
$x_1^2+x_2^2 \geq 0.7$
#Por motivos graficos convirtamos la ecuación anterior parametrizada
#por theta
alpha = np.linspace(0, 2*np.pi)
x1=0.7*np.cos(alpha)
x2=0.7*np.sin(alpha)
X, y = make_circles(
n_samples=100, factor=0.5, noise=0.05, random_state=0)
red = y == 0
green = y == 1
f, ax = plt.subplots(figsize=(4,4))
ax.scatter(X[red, 0], X[red, 1], c="r")
ax.scatter(X[green, 0], X[green, 1], c="g")
plt.plot(x1, x2,"b-")
plt.axis("tight")
plt.xlabel("X_1")
plt.ylabel("X_2")
Text(0, 0.5, 'X_2')
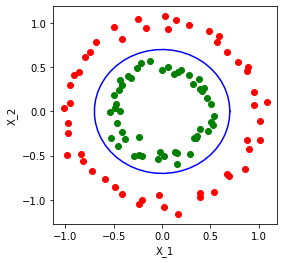
De forma general, ¿Cómo pueden ser elegidos los valores de $\Theta$?.
Para todo el conjunto de datos, tenemos que:
Sea $\Theta^T = [\theta_0,\theta_1,\theta_2,…,\theta_n]$ una matrix $1 \times (n+1)$ y
Para ello, podemos definir la función de coste como :
$ J (\Theta) =\frac{1}{m} \sum_{i=1}^{m} \left[-y\log (h_{\theta}(X ^ {i})) - (1-y)\log (1-h_{\theta}(X^{i})) \right]$
Esta función de coste permite establecer el mejor clasificadose para la regresión logistica de acuerdo a la teroria de probabilidad. Se garantiza que cuando $P(y=1|x,\theta)$ se cumple la función de coste se minimiza, penalizando los valores que sean iguales a $P(y=0|x,\theta)$, analogamente, se cumple que cuando $P(y=0|x,\theta)$ se cumple la función de coste se minimiza, penalizando los valores que sean iguales a $P(y=1|x,\theta)$. La metrica empleada para la regresión lineal no es recomedada en este caso, dado que la funcion de coste puede presentar múltiples minimos que dificultan la minimizacion a través de algunas de las técnicas empleadas. Una justificación adicional para la métrica es dada mas adelante segun la teoria de la probabilidad.
Se deja como tarea motrar que:
Para la demostración, muestre que:
$f(z)=\frac{1}{1+e^{-z}} = f(z)(1-f(z))$
$\frac{\partial h_{\theta}}{\partial \theta_j } = h_{\theta}(X^{(i)})(1-h_{\theta}(X^{(i)}))X_j^{(i)}$
La derivada permite aplicar el gradiente descendente para minimizar nuestra función de coste asi, nuestro algoritmo de minimizacion permite encontrar los valores de $\theta$ despues de un conjunto determinado de itereaciones.
$\theta_j: \theta_j - \alpha \frac{\partial J}{\partial \theta_j}$
Otros metodos de minizacion podrian ser aplicados, tales como:
Interpretación estadística¶
¿Qué tan adeacuado es la elección de $J(\theta)$ para el modelo de regresion logistica?
Asumiendo que los datos de entrenamiento son independientes:
$\cal{L}(\theta)=p(\vec{y}|x, \theta)$
tomando el logaritmo:
Los datos a considerar son los mas probables es decir que para encontrar los valores de $\theta$ que nos garantizan la maxima probabilidad es necesario maximar la función anterior. Despues de realizar los calculos se puede mostrar la ecuación dada para el gradiente de la función de coste.
En conclusión se cumple que:
Para todo el conjunto de datos, tenemos que:
Sea $\Theta^T = [\theta_0,\theta_1,\theta_2,…,\theta_n]$ una matrix $1 \times (n+1)$ y
Función de coste $ J (\Theta) =\frac{1}{m} \sum_{i=1}^{m} \left[-y\log (h_{\theta}(X ^ {i})) - (1-y)\log (1-h_{\theta}(X^{i})) \right]$
Derivada de la funcion de coste
Tomar el iris dataset desde sklearn:
from sklearn import datasets
iris = datasets.load_iris()
Realizar la clasifición de las tres clases a traves de una regresión logística y realizar multiclasicación, para ello considere lo siguiente:
Si en un dataset existen más de 2 clases, $y={0, 1, 2, 3, …}$ se debe construir una multiclasificación, una contra todos, la estrategia sugerida es la siguiente.
Sea A, B, C las tres clases. Para estos valores definir:
Definir la clase A como la clase 0 y todas las otras B, C como la clase 1
Encontrar el valor $h_\theta(X) = P(y=A|x;\theta)$
Definir la clase B como la clase 0 y todas las otras A, C como la clase 1
Encontrar el valor $h_\theta(X) = P(y=B|x;\theta)$
Definir la clase C como la clase 0 y todas las otras A, B como la clase 1
Encontrar el valor $h_\theta(X) = P(y=C|x;\theta)$
from sklearn import datasets
from sklearn.model_selection import StratifiedShuffleSplit
import pandas as pd
from sklearn.linear_model import LogisticRegression
import matplotlib.pylab as plt
iris = datasets.load_iris()
iris.keys()
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])
print(iris.DESCR)
.. _iris_dataset:
Iris plants dataset
--------------------
**Data Set Characteristics:**
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
:Summary Statistics:
============== ==== ==== ======= ===== ====================
Min Max Mean SD Class Correlation
============== ==== ==== ======= ===== ====================
sepal length: 4.3 7.9 5.84 0.83 0.7826
sepal width: 2.0 4.4 3.05 0.43 -0.4194
petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)
petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)
============== ==== ==== ======= ===== ====================
:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.
This is perhaps the best known database to be found in the
pattern recognition literature. Fisher's paper is a classic in the field and
is referenced frequently to this day. (See Duda & Hart, for example.) The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant. One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
.. topic:: References
- Fisher, R.A. "The use of multiple measurements in taxonomic problems"
Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
Mathematical Statistics" (John Wiley, NY, 1950).
- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
Structure and Classification Rule for Recognition in Partially Exposed
Environments". IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-2, No. 1, 67-71.
- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions
on Information Theory, May 1972, 431-433.
- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II
conceptual clustering system finds 3 classes in the data.
- Many, many more ...
iris.target_names
array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
X = iris["data"]
Y = iris["target"]
names_features = iris["feature_names"]
names_target = iris["feature_names"]
df = pd.DataFrame(X, columns=names_features)
df
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 |
| ... | ... | ... | ... | ... |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 |
150 rows × 4 columns
columns_name =[ "".join([c.capitalize() for c in cols.split()]) for cols in df.columns ]
columns_name =[col.replace("(" ,"_") for col in columns_name ]
cols= [col.replace(")" ,"") for col in columns_name ]
df.columns=cols
df["Target"]=Y
df
| SepalLength_cm | SepalWidth_cm | PetalLength_cm | PetalWidth_cm | Target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
| ... | ... | ... | ... | ... | ... |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | 2 |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | 2 |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | 2 |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | 2 |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | 2 |
150 rows × 5 columns
split = StratifiedShuffleSplit(n_splits = 1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(df, df["Target"]):
strat_train_set = df.loc[train_index]
strat_test_set = df.loc[test_index]
df_train = strat_test_set
df_test = strat_train_set
#Clasificación tipo 1: setosa
#Seleccion de valores de y
# Tomemos solo una caractgeristicas por motivos didacticos
y_train = (df_train['Target'] == 0).astype(np.float) # forma rapida, se puede one hot enconder
X_train = df_train.iloc[:,0:1].values
y_test = (df_test['Target'] == 0).astype(np.float)
X_test = df_test.iloc[:,0:1].values
C:\Users\salin\AppData\Local\Temp\ipykernel_27856\2474600366.py:3: DeprecationWarning: `np.float` is a deprecated alias for the builtin `float`. To silence this warning, use `float` by itself. Doing this will not modify any behavior and is safe. If you specifically wanted the numpy scalar type, use `np.float64` here.
Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations
y_train = (df_train['Target'] == 0).astype(np.float) # forma rapida, se puede one hot enconder
C:\Users\salin\AppData\Local\Temp\ipykernel_27856\2474600366.py:6: DeprecationWarning: `np.float` is a deprecated alias for the builtin `float`. To silence this warning, use `float` by itself. Doing this will not modify any behavior and is safe. If you specifically wanted the numpy scalar type, use `np.float64` here.
Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations
y_test = (df_test['Target'] == 0).astype(np.float)
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
LogisticRegression()
print(log_reg.score(X_train,y_train))
print(log_reg.score(X_test,y_test))
0.8
0.9166666666666666
# Determinacion de la frontera
X_new = np.linspace(-10, 10, 1000).reshape(-1, 1)#Generamos los valores de X_new
prob = log_reg.predict_proba(X_new)
prob
array([[1.64601666e-12, 1.00000000e+00],
[1.70552461e-12, 1.00000000e+00],
[1.76703097e-12, 1.00000000e+00],
...,
[9.99731163e-01, 2.68837303e-04],
[9.99740526e-01, 2.59473754e-04],
[9.99749564e-01, 2.50436255e-04]])
decision_boundary = X_new[prob[:, 0] >= 0.5][0]
decision_boundary
array([5.33533534])
plt.figure()
#Regresion Logistica
plt.plot(X_new, prob[:, 0], "g-", linewidth=2, label="Setosa")
# Forntera de desicion
plt.plot(X_train[y_train==0], y_train[y_train==0],"mo",label = "Setosa")
plt.plot(X_train[y_train==1], y_train[y_train==1],"rv",alpha=0.2,label="No Setosa")
plt.xlim(0.0,10)
plt.legend()
plt.vlines(decision_boundary, 0,1)
plt.show()
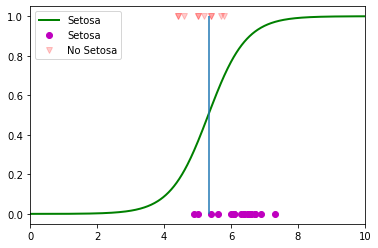
Tarea 8.1¶
¿Entrenar con más caracteristicas y con base a las probabilidades y dado un input definir a que clase pertenece: ‘versicolor’, ‘virginica’ ?
Por ejemplo dado X = [4.9,5.0, 1.8, 0.3] asociados a todas las caracteristicas, ¿cuál es la probabilidad de que la flor sea setosa, versicolor o virginica?
SOFTMAX REGRESION¶
La elección anterior es conocida com softmax regresión, que permite definir un conjunto de probabilidades asociadas a un conjunto de clases. Al definir el maximo valor de la probabilidad dado un conjunto de inputs se tiene el objeto que predice el modelo, una forma de hacer una implementación rapida es mostrada a continuación.
# Para todas las clases se puede realizar facilmente a traves de
# lo siguiente
y_train = df_train['Target']
X_train = df_train.iloc[:,0:1].values
y_test = df_test['Target']
X_test = df_test.iloc[:,0:1].values
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", \
C=10, random_state=42)
softmax_reg.fit(X_train, y_train)
LogisticRegression(C=10, multi_class='multinomial', random_state=42)
X_new = np.linspace(0, 10, 1).reshape(-1,1)
softmax_reg.predict_proba(X)
#Probabilidad de pertencer a la clase cero
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Input In [28], in <cell line: 2>()
1 X_new = np.linspace(0, 10, 1).reshape(-1,1)
----> 2 softmax_reg.predict_proba(X)
File ~\anaconda3\envs\book\lib\site-packages\sklearn\linear_model\_logistic.py:1672, in LogisticRegression.predict_proba(self, X)
1670 return super()._predict_proba_lr(X)
1671 else:
-> 1672 decision = self.decision_function(X)
1673 if decision.ndim == 1:
1674 # Workaround for multi_class="multinomial" and binary outcomes
1675 # which requires softmax prediction with only a 1D decision.
1676 decision_2d = np.c_[-decision, decision]
File ~\anaconda3\envs\book\lib\site-packages\sklearn\linear_model\_base.py:407, in LinearClassifierMixin.decision_function(self, X)
387 """
388 Predict confidence scores for samples.
389
(...)
403 this class would be predicted.
404 """
405 check_is_fitted(self)
--> 407 X = self._validate_data(X, accept_sparse="csr", reset=False)
408 scores = safe_sparse_dot(X, self.coef_.T, dense_output=True) + self.intercept_
409 return scores.ravel() if scores.shape[1] == 1 else scores
File ~\anaconda3\envs\book\lib\site-packages\sklearn\base.py:585, in BaseEstimator._validate_data(self, X, y, reset, validate_separately, **check_params)
582 out = X, y
584 if not no_val_X and check_params.get("ensure_2d", True):
--> 585 self._check_n_features(X, reset=reset)
587 return out
File ~\anaconda3\envs\book\lib\site-packages\sklearn\base.py:400, in BaseEstimator._check_n_features(self, X, reset)
397 return
399 if n_features != self.n_features_in_:
--> 400 raise ValueError(
401 f"X has {n_features} features, but {self.__class__.__name__} "
402 f"is expecting {self.n_features_in_} features as input."
403 )
ValueError: X has 4 features, but LogisticRegression is expecting 1 features as input.
Tarea 8.2¶
Entrenar el modelo anterior para un numero mayor de caracteristicas
Analizar que pasa con la regularaización.
Hacer una analisis de las metricas, construir curvas de aprendizaje para todo el conjunto de datos
Con base en el libro Hand on Machine learning, constrnuir las fronteras de desición para este multiclasificador.
Referencias
[1] http://cs229.stanford.edu/syllabus.html
[2] https://www.coursera.org/learn/machine-learning. Week 3.
[3] https://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html#sphx-glr-auto-examples-classification-plot-classifier-comparison-py
[4]https://scikit-learn.org/stable/datasets/toy_dataset.html